top of page
“C’erano alcune persone su un treno. 19 persone sono scese alla prima fermata. 17 persone sono salite sul treno. Adesso sul treno ci sono 63 persone. Quante persone c’erano sul treno all’inizio?”.

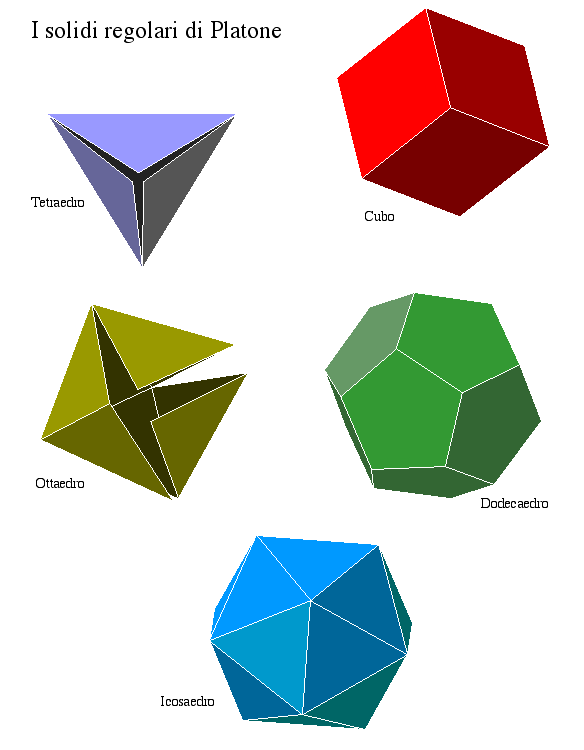
i poliedri regolari, cioè i solidi con facce e lati tutti uguali fra loro sono solo cinque:
il TETRAEDRO o piramide a base triangolare regolare
il CUBO o esaedro
l' OTTAEDRO o bipiramide giustapposta a base quadrata coincidente
il DODECAEDRO a facce tutte pentagonali
e infine l' ICOSAEDRO: 20 facce tutte triangoli equilateri . . . . .
P E R C H E ' ?
perchè se ad un vertice si devono incontrare tre o più facce uguali la somma degli angoli di ciascuna faccia non deve essere 360° o più altrimenti il solido si appiattisce e non si può formare nelle tre dimensioni . . . . . . . .
si incontrano tre o più triangoli: 60° + 60° + 60° = 180°
per non potersi formare occorrono 6 triangoli, ma fino a 5 triangoli si può formare il solido
60°+60°+60°+60°+60°+60° = 360°
infatti esiste il TETRAEDRO e l' ICOSAEDRO
con il quadrato 90° + 90° + 90° si forma l' ESAEDRO o CUBO
ma 90°+90°+90°+90° = 360° niente da fare!
il pentagono ha l' angolo di 108° quindi le uniche due possibilità sono
108° + 108° = 216°
108°+108°+108° = 324° qui è ancora possibile
108° x 4 = 432° qui non più !
INFINE l' esagono non lo consente mai:
120° x 3 = 360°

Nel filmato di Nassin Haramein ognuno dei cinque solidi è inserito nell' altro, in modo che combacino alcune linee(spigoli)
si Parte da un DODECAEDRO, segue un CUBO il cui spigolo combacia con una diagonale del pentagono . . . . .
poi ecco uscire dal CUBO un TETRAEDRO il cui spigolo combacia con la diagonale del quadratofaccia del CUBO . . . . . .
Ecco poi uscire dal nido un OTTAEDRO il cui spigolo coincide con lo spigolo del TETRAEDRO
e infine dall' OTTAEDRO esce un ICOSAEDRO ( il più piccolo dei cinque solidi )

un possibile problema, perfettamente risolvibile potrebbe chiedere allo studente:
SAPRESTI DIRE CHE RAPPORTO C' E' FRA LE AREE TOTALI E POI TRA I VOLUMI DI QUESTI SOLIDI UNO INCLUSO NELL' ALTRO?

problema di geometria solida per la terza classe della secondaria di primo grado


L O G I C A


bottom of page














